Operaciones con polinomios

Suma de polinomios

Para realizar la suma de dos o más polinomios, se debe sumar los coeficientes de los términos cuya parte literal sean iguales, es decir, las variables y exponentes (o grados) deben ser los mismos en los términos a sumar.

Ejemplo:

Suma de los polinomios P(x) = 2x³ + 5x - 3, Q(x) = 4x - 3x² + 2x³.

Método 1 para sumar polinomios:

1. Ordenar los polinomios del término de mayor al de menor grado.

2. Agrupar los monomios del mismo grado.

3. Sumar los monomios semejantes.

Ejemplo:

Paso 1: Ordenamos los polinomios, si no lo están.

P(x) = 2x³ + 5x - 3

Q(x) = 2x³ - 3x² + 4x

Paso 2: Agrupamos los monomios del mismo grado.

P(x) + Q(x) = (2x³ + 5x - 3) + (2x³ - 3x² + 4x)

P(x) + Q(x) = (2x³ + 2x³) + (- 3x²) + (5x + 4x) + (-3)

Paso 3: sumamos los monomios semejantes

P(x) + Q(x) = 4x³ - 3x² + 9x - 3

Método 2 para sumar polinomios:

También podemos sumar polinomios escribiendo una debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.
Paso 1: acomodar en columnas a los términos de mayor a menor grado, y sumar.

2x³           + 5x - 3

2x³ - 3x² + 4x        

4x³ - 3x² + 9x - 3

Paso 2: anotar el resultado
P(x) + Q(x) = 4x³ - 3x² + 9x - 3

Resta de polinomios

La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.

Ejemplo:
Resta de los polinomios P(x) = 2x³ + 5x - 3, Q(x) = 2x³ - 3x² + 4x


Paso 1: obtenemos al sustraendo de Q(x).

P(x) - Q(x) = 2x³ + 5x - 3 - 2x³ + 3x² - 4x

Paso 2: agrupamos.

P(x) - Q(x) = 2x³ - 2x³ + 3x² + 5x - 4x - 3

Paso 3: una vez realizadas las sumas de los monomios semejantes debe anotar el resultado.

P(x) - Q(x) = 3x² + x - 3

Multiplicación de polinomios

Paso 1: Se multiplica cada monomio del primer polinomio por todos los elementos del segundo polinomio.

Paso 2: Se suman los monomios del mismo grado, obteniendo otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.

Ejemplo:

Multiplicación de los siguientes polinomios P(x) = 2x²− 3, Q(x) = 2x³ − 3x² + 4x


Paso 1: Se multiplica cada monomio del primer polinomio por todos los elementos del segundo polinomio.
P(x) · Q(x) = (2x² − 3) · (2x³− 3x² + 4x) = 4x5 − 6x4 + 8x³− 6x³+ 9x²− 12x

Paso 2: se suman los monomios del mismo grado.
P(x) · Q(x) = 4x^5 − 6x^4 + 8x³− 6x³+ 9x²− 12x = 4x^5 − 6x^4 + 2x³ + 9x² − 12x

Paso 3: anotar el resultado.
P(x) · Q(x) = 4x^5 − 6x^4 + 2x³ + 9x² − 12x

División de polinomios:

División del polinomio P(x) = 4x²−8x−2 entre Q(x) = 2x−1.

Paso 1: Escribimos los polinomios:

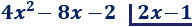
Paso 2: Escribimos 2x en el cociente porque, así, 2x ⋅ 2x = 4x². Multiplicamos el monomio 2x por el divisor y restamos el resultado al dividendo:

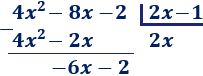
El siguiente monomio del cociente es −3:

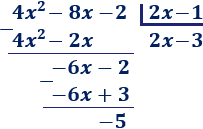
Como el grado del resto es menor que el del divisor, hemos terminado. El cociente es 2x−3 y el resto es −5.